In the previous post on this topic we calculate the probability that a bag of M&M’s was from a certain year based on the distribution of colors. Do do this we derived Bayes’ rule and developed a computational approach to do Bayesian updates. In this blog post we are going to look at a perhaps more realistic case where we should estimate the probability of defective cookies.
How bad is it?
We are one again back at the bakery where we are to estimate the fraction of cookies that are defective (check out this previous post for some background info). To investigate this we took a sample of 50 cookies at random and assessed how many of these cookies that were defective (had a broken ear or similar). In this particular case we found 8 cookies that were defective. Now to the question:
After seeing this data, what can we say about the defect rate?
All Bayesian analysis starts in the same way. We would like to estimate something and for this we use Bayes’ rule. Just as a short recap from the last blog post let’s look at Bayes’ rule
\[ p(H|D) = \frac{p(H) \cdot p(D|H) }{p(D)} \]
where
- \(H\) and \(D\) represent Hypothesis and Data, respectively
- \(p(H)\) is called the Prior which represent our belief about a hypothesis before we see the data
- \(p(H|D)\) is called the Posterior which represents our belief about the hypothesis after we have seen the data. This is the thing that we are interested in.
- \(p(D|H)\) is called the Likelihood and it represents the probability of the data given the hypothesis.
- \(p(D)\) is the probability of getting the data under any hypothesis also called a Normalizing constant
So, let’s start with thinking about the hypothesis, \(H\). In the last blog post on this topic we looked at two bags of M&M’s from two different years. Since they were from two different years they had different distributions of colors. So we had one “parameter”, which year the bag is from, and this parameter could have two different values, 1997 or 2008.
How does that compare to the problem we now are facing? Well, we still have one “parameter”, the defect rate, but in this problem the parameter can take on all the values between 0 (no cookies would be defective) and 1 (all cookies would be defective… not good). We say that the parameter is continuous. So this problem is similar to the previous in one way, just one parameter, but it is different in one way, the parameter is continuous.
Is there a smart way to handle this? Well, yes there is. You can evaluate expression containing funny looking integrals...
... but...
there is also an easy way!
Instead of viewing the parameter as continuous let’s think of it as 101 different hypotheses evenly spaced between 0 and 1. Just like the example with the M&M’s, the hypothesis needs to be mutually exclusive (the defect rate can not be 15% and 32% at the same time) and collectively exhaustive (no other values of the defect rate can be considered). So, the current problem with defective cookies now looks kind of similar to the M&M problem, it just has 101 different hypotheses instead of just two. This means that we can reuse the code that we developed in the last blog post with some “minor” modifications. Nice!
So, once again it is coding time! To define the different hypothesis as a numpy array is simple (here we also do the usual imports)
import numpy as np import matplotlib.pyplot as plt import scipy as sp import seaborn as sns sns.set(context='talk') H = np.arange(0,1.01,0.01)
Now, let’s continue with the data, \(D\). We have collected 50 cookies that could be either OK, non-defective, or defective. To make it simple we represent the defective cookies with the letter ‘D’ and the non-defective ones with ‘N’.
D = ['N','N','N','N','D','N','D','N','N','N','N','N','N','N','N','N','N','N','N','N','D','D','N','N','N', 'N','N','N','N','N','N','N','D','D','N','N','N','D','N','N','N','N','N','D','N','N','N','N','N','N']
Now, let’s look at the prior i.e what is our belief about the defect rate before we see this new data (the 50 cookies that we collected). For now we just assume that all of the 101 possible values for the defect rate are equal as likely, this is called a non-informative prior.
prior = np.ones(len(H)) prior = prior/np.sum(prior)
OK, so far so good. Now comes the more tricky part, the likelihood function. The likelihood function p(H|D) returns the probability of the hypothesis given the data. So, as an example, you can ask this question: if the probability of getting a defective cookie is 30% (the hypothesis) what is the probability of getting a defective cookie (the data)... hmmm… better read that again? Well, after reading the question a few times, it is actually as simple as you think, it is 30%. And by the same way of thinking: if the probability of getting a defective cookie is 30%, what is the probability of getting an OK cookie? Well, it must be 70%. So, let’s write that in code.
def likelihood(d,h): if d == 'N': p = 1 - h else: p = h return p
Believe it or not but we are now ready to do the Bayesian updates using the same code as developed in the previous blog post. Remember that the posterior for one datapoint acts as the prior for the next data point.
posterior = np.ones(len(H)) Prior_plot = [] Posterior_plot = [] Posterior_plot.append(prior) for i in range(0,len(D)): # loop over all data point d = D[i] for j in range(0,len(H)): # loop over all hypotheses h = H[j] posterior[j] = prior[j] * likelihood(d,h) posterior = posterior/np.sum(posterior) Prior_plot.append(np.copy(prior)) Posterior_plot.append(np.copy(posterior)) prior = np.copy(posterior) # plot the results plt.figure(figsize=(15,18)) counter = 1 for jj in [0,1,2,3,5,10,30,50]: plt.subplot(4,2,counter) counter = counter + 1 #plt.figure(figsize=(6,3)) plt.plot(H,Posterior_plot[jj],'r',lw=3) plt.fill_between(H,Posterior_plot[jj],0,color='r',alpha=0.1) plt.ylim(-0.0005,0.11) plt.text(0.55,0.09,'Sample size = ' + str(jj)) plt.text(0.39,0.075,'# defective cookies = ' + str(np.sum(np.array(D[:jj])=='D'))) if counter < 4: plt.title('Posterior') if counter >7: plt.xlabel('Defect rate [-]') plt.ylabel('Probability [-]') plt.show()
Below you have a small animated gif that shows what is going on during all the steps of the Bayesian update
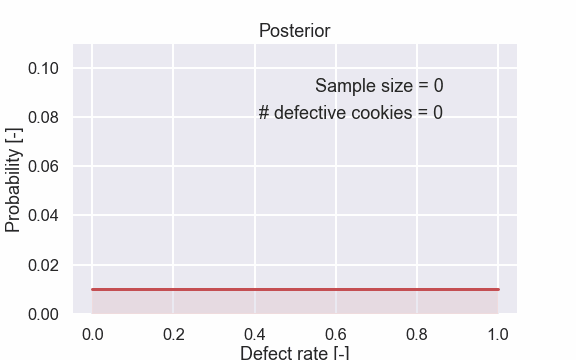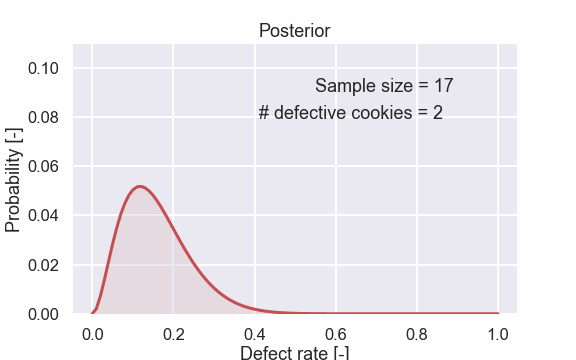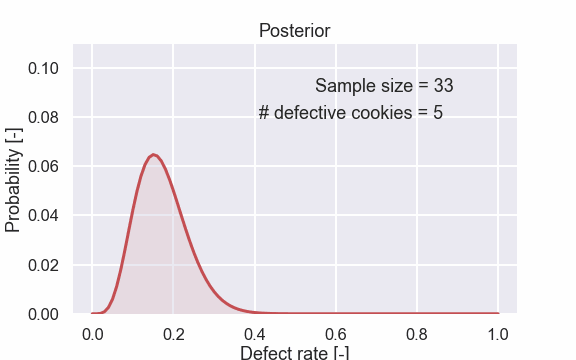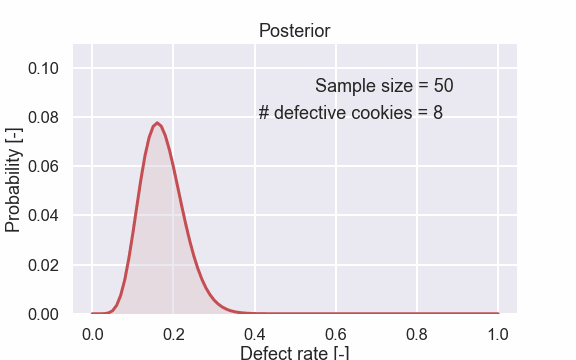
Here are also some of the plots.
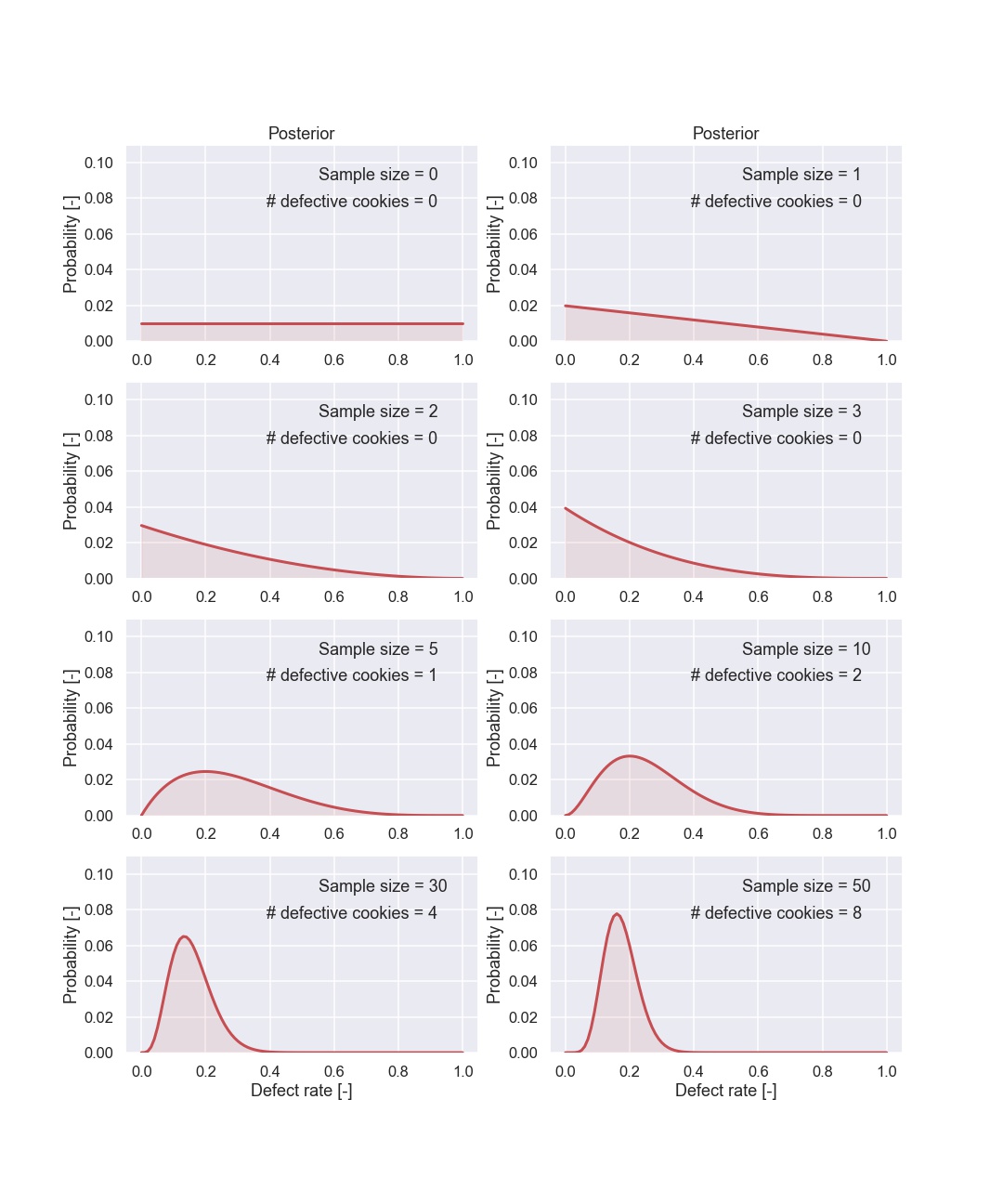
Let’s start with the first plot. Remember that the prior is flat i.e. all the possible defect rates are just as likely. After seeing one cookie that was non defective we can conclude that the probability of 100% defect rate is 0%. I know, it is a bit awful to talk about the probability of a probability but think of the defect rate as just a number. Moreover, after seeing one cookie we think that the defect rate of 0% is the most probable one. Now, let’s have a look at the second figure where we have seen the result from the second cookie.
Also the second cookie was non defective, so we still think that a defect rate of 0% is the most probable value, moreover we are now more certain compared to “just” seeing one cookie. Still, two cookies is not that much data and this is directly shown by the width of the probability distribution.
So let’s look at some more cookies. The fifth picture shows the posterior after seeing 5 cookies, 1 defective and 4 that are OK. So, now we have seen a cookie that is defective so the probability of 0% defective cookies can be ruled out. This is seen in the figure since the probability of 0% defect rate is very low (it is actually 0).
From the different figures above it is clear that the distribution gets more and more “narrow” as the sample size increases. This is handled automatically by the Bayesian update.
Now, let’s have a close look at the final result for 50 tested cookies. Let’s make a larger plot so we can see what is going on.
The value 16% is the most probable and that kind of makes sense since it is the same as 8/50. We can also see that values above say 25% and values below 10% are kind of unlikely.
So the width of the distribution tells you something about how certain you are about the value of the parameters. A nice way to communicate this is to calculate a credibility interval. A 90% credibility interval represents an interval that there is a 90% probability that the parameter is within the given bounds. To calculate this we can simply look at the cumulative sum of the posterior and find the 5% and 95% percentiles
plt.figure(figsize=(10,6)) plt.plot(H,np.cumsum(Posterior_plot[50]),'r',lw=3) plt.xlabel('Defect rate [-]') plt.title('Cumulative distribution function of posterior') plt.ylabel('Probability [-]') plt.show()
and the plot
After identifying the values that are closest to 5% and 95% we get an credibility interval of [0.09, 0.26].
Just for fun, let’s mark the 90% credibility interval in the same figure as the posterior.
So 90% of the probability is within the shaded area. After calculating this interval you can actually say there is a 90% probability that the parameter is within the reported interval. This is, strictly speaking, not true for a confidence interval that we have talked about in a previous blog post. I’m not going to write more about the difference between a confidence interval and a credibility interval. This is, or at least can be, a very deep hole and involves more philosophical discussions regarding the frequentist vs. Bayesian view of the world.
If you find this interesting there are tons of material online just a few google searches away.
I Know the Process so Well
In the previous calculations we used a non informative prior i.e. we assumed that all values of the defect rate were just as likely. Well, this is sometimes a reasonable thing to assume but here we “miss out” of something good with this way of analysing things. Through the prior we have a golden opportunity to incorporate any prior knowledge we might have of the process. In this case we might talk to the person who runs the bakery and hear what he/she has to say. The person might say something like:
Well I have been making this type of cookie for a long time and it is really difficult to get those ears to look nice. I think that we have a lot of cookies that look bad, perhaps not 50% but not that far away from it. I can not remember that we have ever made a batch of 50 cookies and all 50 were ok.
This seems to be valuable information but how to incorporate this into the analysis? Well, the prior can be used for just this purpose.
The problem is how to transform an “opinion” like the one above into something that can be used in the bayesian update.
As you may have figured out there is no unique way of doing so but let’s give it a try anyway!
Let’s have a look at something called a beta distribution. A beta distribution has two parameters, \(\alpha\) and \(\beta\), that together determine the shape of the distribution. The beta distribution is defined between 0 and 1 (including both) so it seems to fit well as a prior for the problem at hand.
Let's make a plot of the beta distribution for some different values of \(\alpha\) and \(\beta\).
example_beta = [[1,1],[5,5],[5,1],[2,9]] plt.figure(figsize=(10,6)) for params in example_beta: beta_dist = sp.stats.beta.pdf(H,params[0],params[1]) beta_dist = beta_dist / np.sum(beta_dist) plt.plot(H,beta_dist,label='alpha = ' + str(params[0]) + ', beta = ' + str(params[1])) plt.fill_between(H,beta_dist,0,alpha=0.1) plt.xlabel('Defect rate [-]') plt.ylabel('Probability [-]') plt.title('Beta distribution') plt.legend() plt.show()and the result
Ok, it looks like you can get all kinds of shapes by changing the values of \(\alpha\) and \(\beta\). Now, let’s try to get a distribution that sort of resembles the information that we got above from the person working at the bakery. Below there is a figure for a beta distribution with \(\alpha = 3\) and \(\beta = 8\)
Not too bad I would say. There is a low probability that the defect rate is zero and values above say 60% are unlikely. A different person would most likely have chosen a slightly different set of parameters but for the moment let’s try this one out.
So, Now we can use this prior as a starting point for the Bayesian update. Let’s write it in code
prior = sp.stats.beta.pdf(H,3,8) prior = prior/np.sum(prior) posterior_2 = np.ones(len(H)) for i in range(0,len(D)): d = D[i] for j in range(0,len(H)): h = H[j] posterior_2[j] = prior[j] * likelihood(d,h) posterior_2 = posterior_2/np.sum(posterior_2) prior = np.copy(posterior_2) posterior_2 = posterior_2/np.sum(posterior_2)
Well done, Now, just to end this analysis, let’s plot the two different posterior distributions, one with a non informative prior and the other with an informative prior.
Super! As you can see, the difference between the two different posterior distributions is not that large in this case. The reason for this is that, in this case, we had quite a lot of data. With enough data, two persons with different initial opinions of the defect rate will end up with similar beliefs after seeing the data. This is sometimes referred to as swamping the prior.
Just to show this, let’s also include a plot where we compare the two different posterior distributions when we only have seen data for 5 cookies.
Here it is more clear that the initial belief has an impact on the posterior distribution.
Time to conclude
Ok, yet another blog post has come to its end. In this blog post we were able to estimate the defect rate of certain cookies using Bayes’ rule. We also defined a credibility interval that actually means there is a 90% (or any other number) probability that the parameter is within the given interval.
Since we used a computational approach we could solve this problem fairly easy even though the parameter in this case was continous. We solved it by dividing the interval in many points (this is often called a gridding technique). In this case we used steps of 1% unit since this was ok resolution for our purpose. If better resolution is needed then we could divide the interval in more points, at a higher computational cost of course.
In the next blog post on this topic we will have a look on how to do inference, so stay tuned.
As always, feel free to contact us at info@gemello.se