Back from vacation and some new topics to write about. This is the first blog post in a series of (probably) three about something called Principal Component Analysis or PCA. So what is it and what can it be used for?
In this first post the idea is to get a feel for what PCA is all about.
Let's look at some (fake) data
It is often easier to explain things when we look at an example so let’s load some (made up) data and get going (we will look at some “real” data in the upcoming blog posts).
x_1 = np.array([3.99975647, 1.52664636, 2.11809712, 5.08688 , 9.26157043, 6.26779231, 7.69514263, 3.61320641, 3.78624789, 5.14279517, 4.15163416, 6.55947791, 6.72778074, 4.74686023, 4.83100059, 3.84360628, 3.17224213, 9.17148181, 6.49046084, 3.7469048 , 6.4779173 , 6.08749411, 7.87593261, 5.835298 , 8.37203072, 1.94751049, 9.80599024, 2.90854427, 4.30802596, 5.60590441, 6.04012403, 1.83037242, 6.16341386, 1.85196674, 4.99910719, 4.36183203, 2.57058315, 2.55768456, 6.92334994, 5.15661497]) x_2 = np.array([1.57412994, 1.5013287 , 0.11684484, 3.94805052, 9.29820217, 3.62782632, 5.45556552, 1.37605334, 2.11222349, 4.46800798, 1.74776468, 5.11406232, 4.2433477 , 3.70217321, 2.33703761, 3.04097556, 3.25911705, 5.78395499, 5.82535278, 3.02558801, 3.27760297, 5.51091845, 3.30858429, 3.58055778, 5.59313903, 3.28897547, 7.66201726, 1.30855073, 3.08531934, 3.82434618, 1.45557186, 0.64359249, 3.40996942, 1.35878049, 3.60808153, 2.83268186, 1.64319734, 0.4549066 , 3.27352886, 3.97796542]) plt.figure(figsize=(8,8)) plt.scatter(x_1,x_2,c='r',edgecolor='k',alpha=1.0) plt.axis('equal') plt.xlabel('x_1') plt.ylabel('x_2') plt.show()
So a data set that contains 40 points and for each point we have measured two properties called \(x_1\) and \(x_2\). This is what the scatter plot of the data looks like
As can be seen from the plot there seems to be some relationship between the variable \(x_1\) and the variable \(x_2\) since the points are distributed sort of along the diagonal. Now, before we start with the actual PCA stuff lets do a small modification of the data. We simply remove the mean value for each of the two variables and create two new variables called \(x_1’\) and \(x_2’\). It would look like this
x_1_prim = x_1 - np.mean(x_1) x_2_prim = x_2 - np.mean(x_2) plt.figure(figsize=(8,8)) plt.scatter(x_1_prim,x_2_prim,c='r',edgecolor='k',alpha=1.0) plt.axis('equal') plt.xlabel('x_1´') plt.ylabel('x_2´') plt.show()
and the plot
So we have just “moved” the data so it is centered around zero. The reason for doing this will be more clear as we go along.
One Direction is the "best"
Now, perhaps you have heard about a thing called variance. Variance measures how far a set of numbers is spread out from their average value and can be calculated as
\[ Var(x) = \frac{1}{n-1} \sum{(x_i - \mu)^2} \]
where \(µ\) is the average value of \(x\) defined as
\[ \mu = \frac{1}{n} \sum{x_i} \]
Let’s look at the variance for \(x_1’\) and \(x_2’\). Since the mean of each of our two variables are zero (by construction ) the mean term in the expression for the variance can be "removed". This means that we can calculate the variance of \(x_1’\) by this compact formula
\[ Var(x_1') = \frac{1}{n-1} \sum{(x_1')_i^2} \]
Ok, so far so good. Now the fun part begins. Let’s imagine a line going through the point (0,0) in the graph above. At the moment the direction of the line is arbitrary but let’s look at one possible direction and plot it in the same graph as above.
The next steps might seem strange at first but (hopefully) it will all make sense in the end.
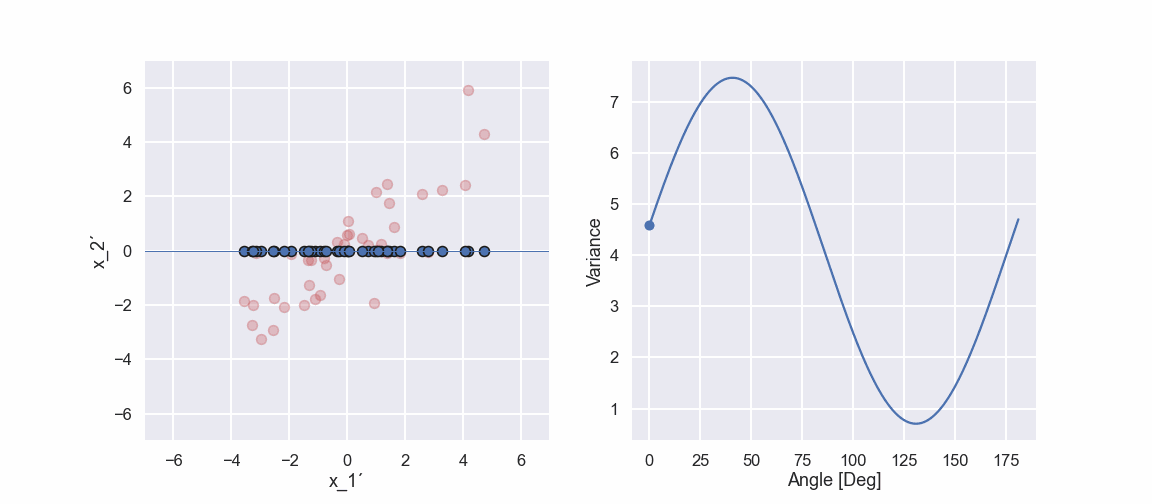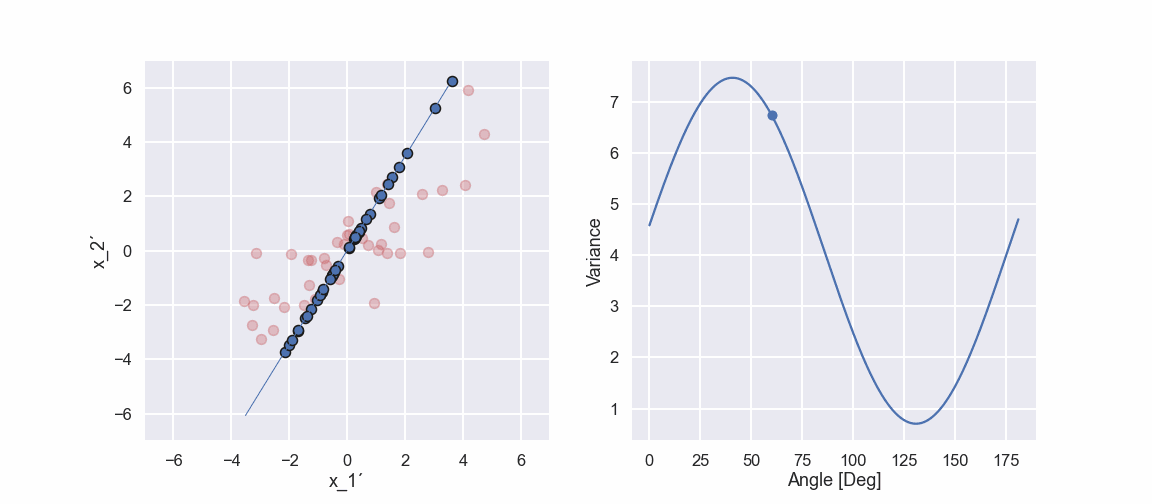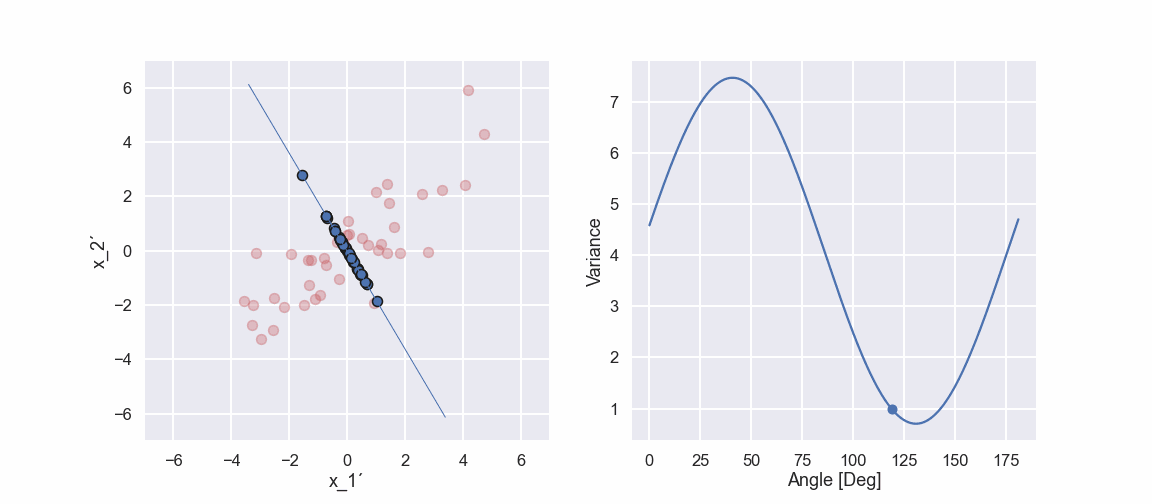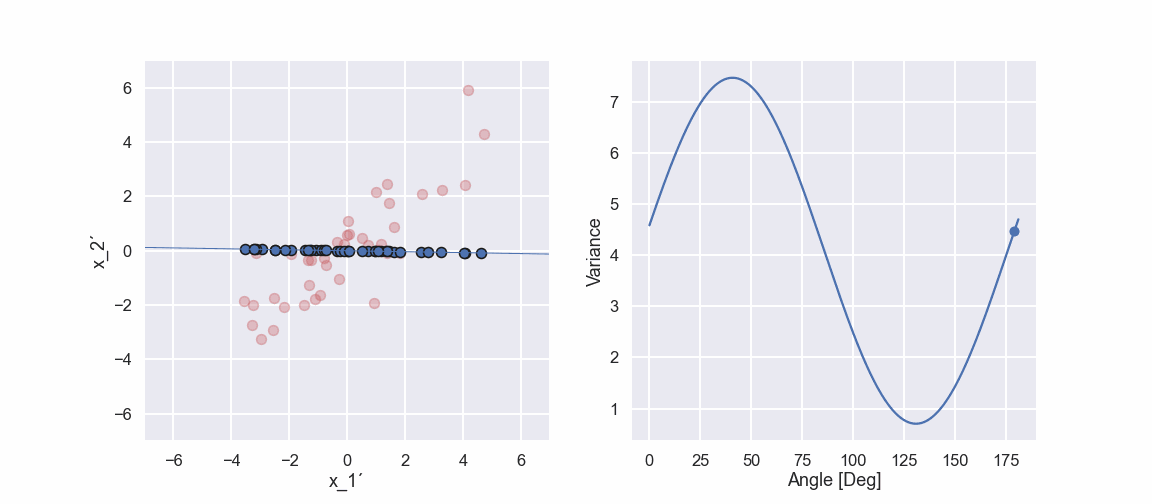
Let’s project one of the data points on this shoosen direction.
Note that the projection is perpendicular to the direction given by the blue line. The black line is the distance from the origin to the projected point (in the shoosen direction). Now we continue by doing a similar projection for all 40 data points, it would look something like this
Ok, let’s do the same projection stuff in a different direction
So, if we compare the two last pictures we see something interesting. The projected points (blue points) are more spread out in one direction when compared to the other direction. This would mean that the variance is higher in one direction compared to the other direction. Note that if we did the projection in the vertical direction and calculated the variance we would get the variance of the \(x_2'\) variable.
A sort of natural question to ask now is:
Is there a direction where the variance is as large as possible?
Well... it seems reasonable that such a direction would exist. Let’s try to answer this question by just looping over a large number of directions and for each direction calculate the variance.
Before we do that, just a short note on how to calculate the coordinate of the data points in a specific direction. The mathematical tool that we will be using is the scalar product which by definition will give us the thing that we are looking for (if the direction is represented by a unit vector i.e. length 1)
The scalar product can be calculated by the function numpy.dot()
Now, some code to calculate the variance in all the different directions and a plot to show the result. Here the direction is represented by an angle measured from the x_1’ coordinate axis.
variation_ang = [] proj_angle = np.linspace(0,181,400) for bb in proj_angle: aa = bb * np.pi / 180 direction = np.array([np.cos(aa),np.sin(aa)]) proj_dir = [] for i in range(0,len(x_1_prim)): proj = np.dot(direction,np.array([x_1_prim[i],x_2_prim[i]])) proj_dir.append(proj) variation_ang.append(np.var(proj_dir)) plt.figure(figsize=(10,7)) plt.plot(proj_angle,variation_ang) plt.xlabel('Angle [Deg]') plt.ylabel('Variance') plt.show()
and the plot
Ok, we can see that there is a maximum of the variance at approximately 41 deg. Moreover, the variance seems to have a minimum value at approximately 131 deg. Hmm that is like 90 deg difference… interesting... we will get back to that in an upcoming blog post.
Just to summarize the investigation we just did I have included a small animated gif below.
So, we have found a direction that maximizes the variance of the data, Nice! Let’s call this direction something catchy, why not the first principal component. It is called the first principal component because it is connected to the direction of largest variance. How do we then get the second principal component? This direction should also maximize the variance but also be orthogonal (perpendicular) to the first principal component. Well, since this is a two dimensional example (just to make it easy) the second principal component is directly given by the orthogonality constraint. If the example would have 3 variables we would need to do a similar search among directions perpendicular to the first direction in order to find the one with the largest variance and then the third direction is perpendicular to both the first and the second principal component.
So... now we have found the principal components. Awesome!
What we can do next is to “recast” the data along the principal components axes. This we do just by projecting the data onto the directions of the first and second principal component.
a_1 = ang_max_var *np.pi/180 a_2 = ang_min_var *np.pi/180 direction_1 = np.array([np.cos(a_1),np.sin(a_1)]) * 1 direction_2 = np.array([np.cos(a_2),np.sin(a_2)]) * 1 proj_1_vector = [] proj_2_vector = [] for i in range(0,len(x_1_prim)): proj_1 = np.dot(direction_1,np.array([x_1_prim[i],x_2_prim[i]])) proj_2 = np.dot(direction_2,np.array([x_1_prim[i],x_2_prim[i]])) proj_1_vector.append(proj_1) proj_2_vector.append(proj_2) plt.figure(figsize=(16,7)) plt.subplot(1,2,1) plt.scatter(x_1_prim,x_2_prim,c='r',s=100,alpha=1.0,edgecolor='k') plt.xlim(-8,8) plt.ylim(-8,8) plt.xlabel('x_1´') plt.ylabel('x_2´') plt.subplot(1,2,2) plt.scatter(proj_1_vector,proj_2_vector,c='r',s=100,edgecolor='k') plt.xlim(-8,8) plt.ylim(-8,8) plt.xlabel('PC_1') plt.ylabel('PC_2') plt.show()
and the plot looks like this
So, what has happened here? The data looks kind of similar, it is sort of “rotated” so the largest variance is along the axis of the first principal component. So, in one way we have just changed the coordinate system the we use to describe the location of each data point, i.e. we have smashed a fraction of \(x_1'\) together with a different fraction of \(x_2’\) and called this combination the first principal component.
Moreover, in the original plot we can see that the points are sort of located along the diagonal. This indicates that there is some relation between the first and second variable. In the plot to the right, however, we do not have this orientation. This means that when showing the data in this way the relation between the two principal components is not seen, we will also get back to this in the upcoming blog post on this topic.
Time to conclude
Ok, this was the first blog post on the topic Principal Component Analysis or PCA. The idea was to give some sort of intuition of what PCA is about.
In the next blog post we are going to have a short look at the mathematical background to PCA. This will, in the end, give a much more efficient way to calculate the principal component, especially if we have a lot of variables.
Well that was all for this time! As always, feel free to contact us at info@gemello.se