So, time for a new blog post. This one would probably fall in the category called: An engineering solution to a non engineering problem. We are going to solve a Sudoku puzzle using python.
How to play Sudoku?
Ok, first of all, what is Sudoku? I found the following description on Wikipedia:
In classic sudoku, the objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 subgrids that compose the grid (also called "boxes", "blocks", or "regions") contain all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.
Alright, sounds like a fun game. Let’s have a look at an example to get an even better understanding of what it is. Below is an example of the starting point of a Sudoku puzzle.
So, some digits are given and the idea of the game is to fill in all the gaps with a digit from 1 to 9 that fulfills all the rules given above. Let’s have a look at a specific gap
So, we are trying to figure out which digit (1-9) that can be placed in the gap marked by the “?” . A digit can only appear one time for each row, column and 3X3 subgrid Let’s start with the row, here we have the digits 1, 2, 3 and 9 so these digits are not allowed. Looking at the column we find in addition to the 1, 2, 3 and 9 (that were in the row) also 5 and 7. So at the moment we have ruled out the digits 1, 2, 3, 5, 7 and 9 as possible options. Finally, looking at the subgrid we also find the digit 8 i.e. in total we have found 1, 2, 3, 4, 5, 7, 8 and 9. This brings us to the conclusion that the digit 6 is the only possible option since it is not present in the same row, column or subgrid.
Sometimes it is not that straightforward… let's look at a different gap.
So, what do we have here? In the row we have the digits 2, 3 and 6, in the column we have in addition 5, 7 and 8 and in the subgrid we have no additional digits. This would mean that we have 1, 4 and 9 as possible options so at this moment we are not sure of what digit to fill in.
Now that we have understood how to play Sudoku let’s think how we can solve it using python.
How to solve a Sudoku using python?
Before we start with some coding let’s think about how one can solve a Sudoku puzzle.
The first option that comes into my mind is to try a brute force approach where we basically do a for loop from 1 to 9 for each gap in the puzzle. For each possible combination we then check all rows, columns and subgrids so each number from 1 to 9 exists.
The second option could be something similar to how a human would solve this problem i.e. be really clever on where to put in digits.
In this blog post we are not going to use one of the above strategies but rather something in between a really dumb strategy and a really clever strategy. We are going to use something called backtracking which, according to Wikipedia, is described as:
Backtracking is a general algorithm for finding solutions to some computational problems, that incrementally builds candidates to the solutions, and abandons a candidate ("backtracks") as soon as it determines that the candidate cannot possibly be completed to a valid solution.
What does this backtracking thing mean then… Well on a general level, the strategy is very similar to solving a maze like the one below.
You start walking in one direction and arrive at a point where you have several directions to choose from. At this point you choose one direction, the important thing here is not which direction you choose but it is important that you remember it. You continue like this until you get stuck in a dead end and here the main idea of the backtracking strategy can be demonstrated.
So what you do is to go back to the last point where you made a decision on where to go. Here you remember what directions you already have tried and see if there are other directions that you have not yet tried. If there is a direction that you have not tried yet you continue in this direction (no surprise here) but what to do if you already have tried all possible directions?
Well, then you have to continue to go even further back to the next point where you made a decision and see what possibilities exist there. If there is a possible direction that has not yet been tried you continue in this direction, if not you have to go back to the previous point where you had to make a decision about your path.
Then you continue like this until you have reached the end and voila you are done!
OK, this seems like a very natural strategy, but how do we transfer this general strategy with the maze analogy to our Sudoku puzzle?
Well, something like this:
- Find an empty gap in the grid
- Fill in the first digit that is possible (start checking from 1)
- If it is not possible to fill in any digit, leave the gap empty and go back to the previous gap you filled in and check if a different digit is possible to fill in.
- If it is possible, continue. If not, leave the gap empty and go back.
This then continues until the complete Sudoku is filled in. And we are done!!
If we compare this backtracking strategy to the sort of naive brute force strategy that was suggested in the beginning of this blog post, it is clear that this strategy is much more efficient. The main reason is that as soon as we understand that the current grid can not be completed we directly abandon this grid and move backwards to change it.
Now that we have sorted out the strategy we would like to use, let’s start to code!
Time to do some coding!
Now the really fun part begins. First of all some needed imports and then we define the partially completed grid (here called board)
import numpy as np import matplotlib.pyplot as plt import seaborn as sns sns.set(context='talk') board = np.array( [[np.nan, 2., np.nan, np.nan, 7., 3., np.nan, np.nan, np.nan], [np.nan, 5., np.nan, 2., 9., 1., 7., 3., 8.], [ 7., np.nan, 3., np.nan, 5., np.nan, 4., 2., 9.], [np.nan, np.nan, np.nan, np.nan, 6., np.nan, np.nan, np.nan, np.nan], [np.nan, np.nan, np.nan, np.nan, 3., 2., 6., np.nan, np.nan], [ 2., 8., 6., 5., np.nan, 4., np.nan, 7., np.nan], [np.nan, 7., np.nan, 3., np.nan, np.nan, 8., 5., 1.], [np.nan, np.nan, np.nan, 1., 2., 9., 3., np.nan, np.nan], [ 3., np.nan, 1., 7., np.nan, np.nan, 2., 9., 4.]])
Here we have used the numpy.nan presentation of Not a Number for the gaps in the grid that do not yet have a number.
Next step is to define some small helper functions that will come in handy later on. The first one is just a plotting function that takes the board as input parameter and makes a “nice” plot of it.
def plot_board(board): plt.figure(figsize=(8,8)) sns.heatmap(board,linewidths=.5,annot=True,cmap='viridis',cbar=False) plt.plot([0,10],[0,0],'r',lw=4) plt.plot([0,10],[3,3],'r',lw=4) plt.plot([0,10],[6,6],'r',lw=4) plt.plot([0,10],[9,9],'r',lw=4) plt.plot([0,0],[0,10],'r',lw=4) plt.plot([3,3],[0,10],'r',lw=4) plt.plot([6,6],[0,10],'r',lw=4) plt.plot([9,9],[0,10],'r',lw=4) # predefined numbers XX = [1.5,4.5,5.5, 1.5,3.5,4.5,5.5,6.5,7.5,8.5, 0.5,2.5,4.5,6.5,7.5,8.5, 4.5, 4.5,5.5,6.5, 0.5,1.5,2.5,3.5,5.5,7.5, 1.5,3.5,6.5,7.5,8.5, 3.5,4.5,5.5,6.5, 0.5,2.5,3.5,6.5,7.5,8.5] YY = [0.47,0.47,0.47, 1.47,1.47,1.47,1.47,1.47,1.47,1.47, 2.47,2.47,2.47,2.47,2.47,2.47, 3.47, 4.47,4.47,4.47, 5.47,5.47,5.47,5.47,5.47,5.47, 6.47,6.47,6.47,6.47,6.47, 7.47,7.47,7.47,7.47, 8.47,8.47,8.47,8.47,8.47,8.47] plt.scatter(XX,YY,s=800,facecolors='none',edgecolors='w') plt.show()
If we run plot(board) we get something like this
The circles around the predefined number are just there to make the visualization more clear when we start to actually solve the Sudoku puzzle.
The next helper function is a function that checks if a certain number (1-9) can be placed in a certain gap of the grid. The input parameters to this function are the board, the number to test and the position in the grid of the number that should be tested. The function will return True if it is possible and False otherwise.
def is_valid(board,number,pos): # check row if np.sum(board[pos[0],:]==number)>0: return False # check col if np.sum(board[:,pos[1]]==number)>0: return False # check 3X3 square start_row = pos[0] // 3 * 3 start_col = pos[1] // 3 * 3 if np.sum(board[start_row:start_row+3,start_col:start_col+3]==number)>0: return False return True
Just some short words on this function. We would like to know if this number already exists in the same row, column or 3X3 sub grid. So let’s try it out! If we look at column 8 and row 8 we saw earlier that the only possible number that could be inserted here and still fulfill all the conditions was 6. So, let’s try all numbers from 1 to 9 and see what happen
for i in range(1,10): print(str(i) + ': ' + str(is_valid(board,i,[7,7])) )
Alright! Seems like we are ready to proceed.
To solve this, we are going to use something really nifty, something called recursion. Let’s write down the code and have a look at it.
def solve(board): for x in range(9): for y in range(9): if np.isnan(board[y,x]): for n in range(1,10): if is_valid(board,n,(y,x)): board[y,x] = n solve(board) board[y,x] = np.NaN return plot_board(board)
Believe it or not but that is it!
So what is going on here?
- Loop over all positions in the grid
- check if the gap is empty
- If it if empty start to test numbers to see if it fulfills all constraints
- If you find a number that is valid, put it in the gap and start from the beginning I.e. we call the same function again (Recursion)
- If we can not find any valid number put in a np.NaN that represents an empty gap and go back to the last previous position where you put in a number and try to find a different number that is valid
The “trick” here is that we call the function itself inside the function.
If we run the code solve(board) we get this output
This looks really nice, each row, column and subgrid all contains all numbers from 1 to 9. Excellent!!
Just to get some more visualization of the backtracking strategy we look at an animated gif where all steps for solving this puzzle are shown
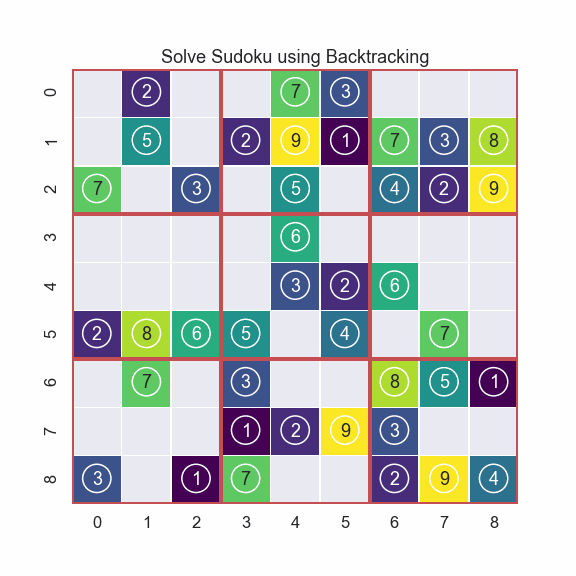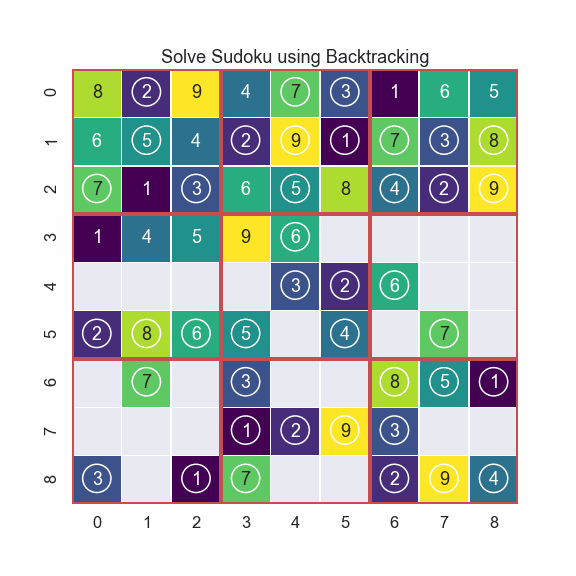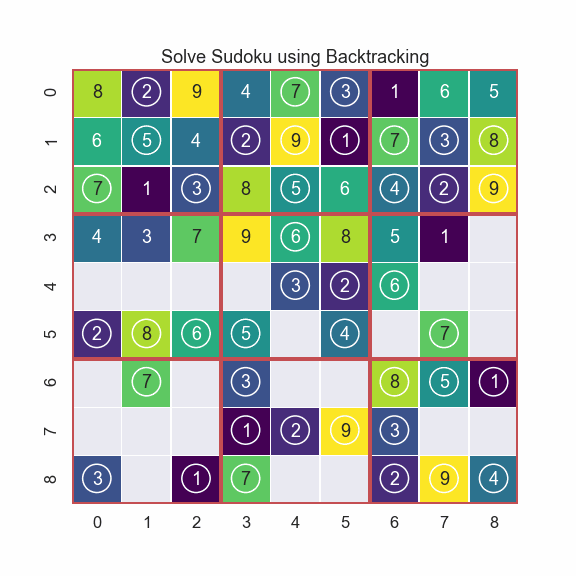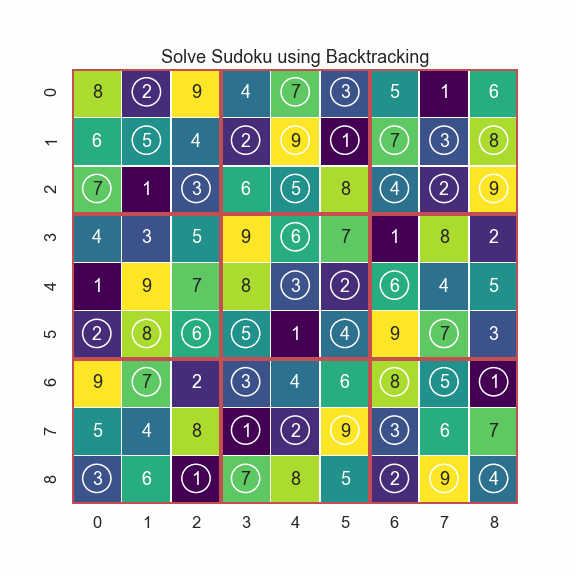
Sweet! You can clearly see how the algorithm works. When we can not move forward we move backward and try a new number.
Time to conclude
So, perhaps not the most engineering problem you have seen but, at least to me, it was a quite fun problem to solve. We saw that this backtracking strategy is efficient (at least when compared to a sort of naive brute force strategy) and quite easy to implement. Just remember that a game of Sudoku can be fun to solve on your own as well :-)
As always, feel free to contact us at info@gemello.se