Golf can be a frustrating game. Even when you finally reach the green (and the possibility to lose a golf ball into the woods is quite small), the putting game can also put some stress on your mind.
In this blog post, the art of putting will be investigated. This post will be the first of two, and in this part the main focus will be:
Can the game of putting be modelled using basic mechanics?
Of course, I am not the first guy to ask this question. The material in this post is taken from this great article. So without further ado let's get started!
Let's get mechanical
The good thing about mechanics is that if only a limited set of principles are mastered, great things can be accomplished. Basically, to set up the problem, all we need is three equations
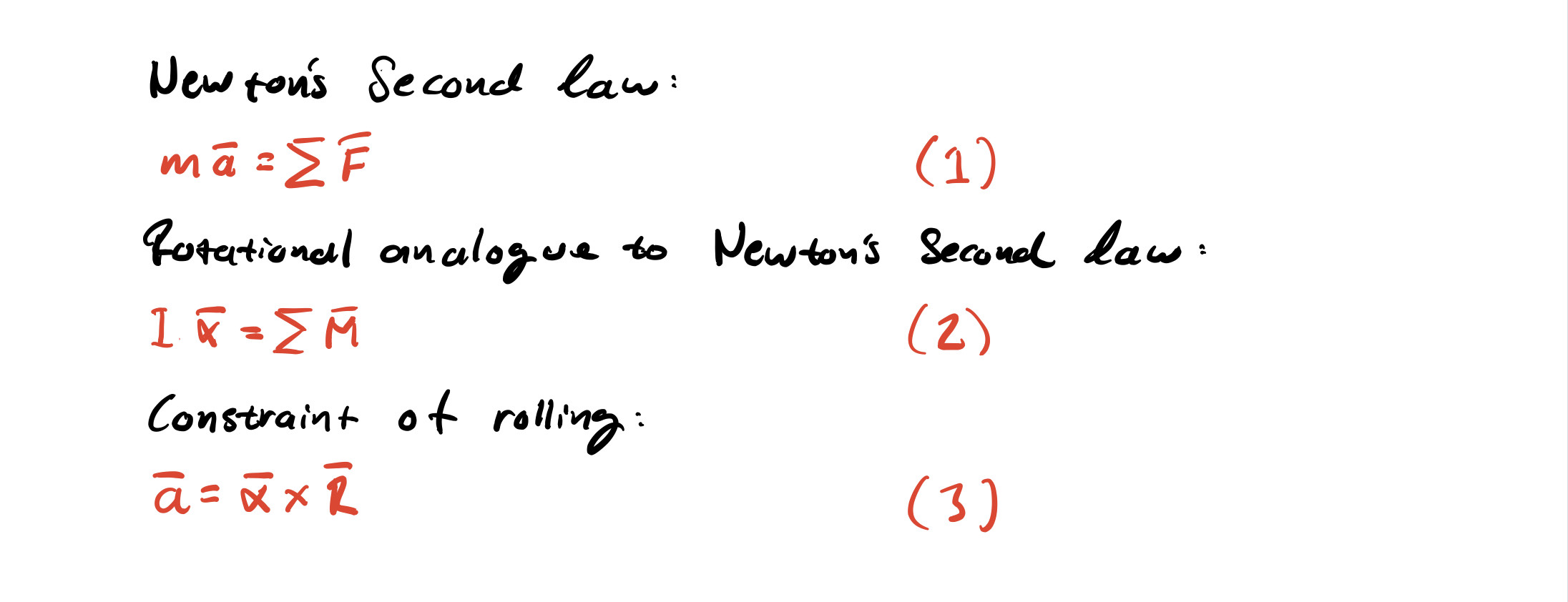
If someone has difficulty reading my handwriting, sorry for that. Nevertheless, the first equation simply states that the sum of forces is equal to mass times acceleration. The second equation is kind of similar, but states that the sum of moments are proportional to angular acceleration. In addition, since the golf ball is assumed to be rolling on the green, a one to one relation between the angular acceleration and acceleration can be made. This if found in the third equation.
OK, that’s great, now what? In most mechanical problems, a good picture of the problem is a good starting point and this also holds for this problem. Below (right) you can see a sketch of the golf ball from above. In this case the z-axis is normal to the putting surface of the green. Left is the above equations resulting from the picture.
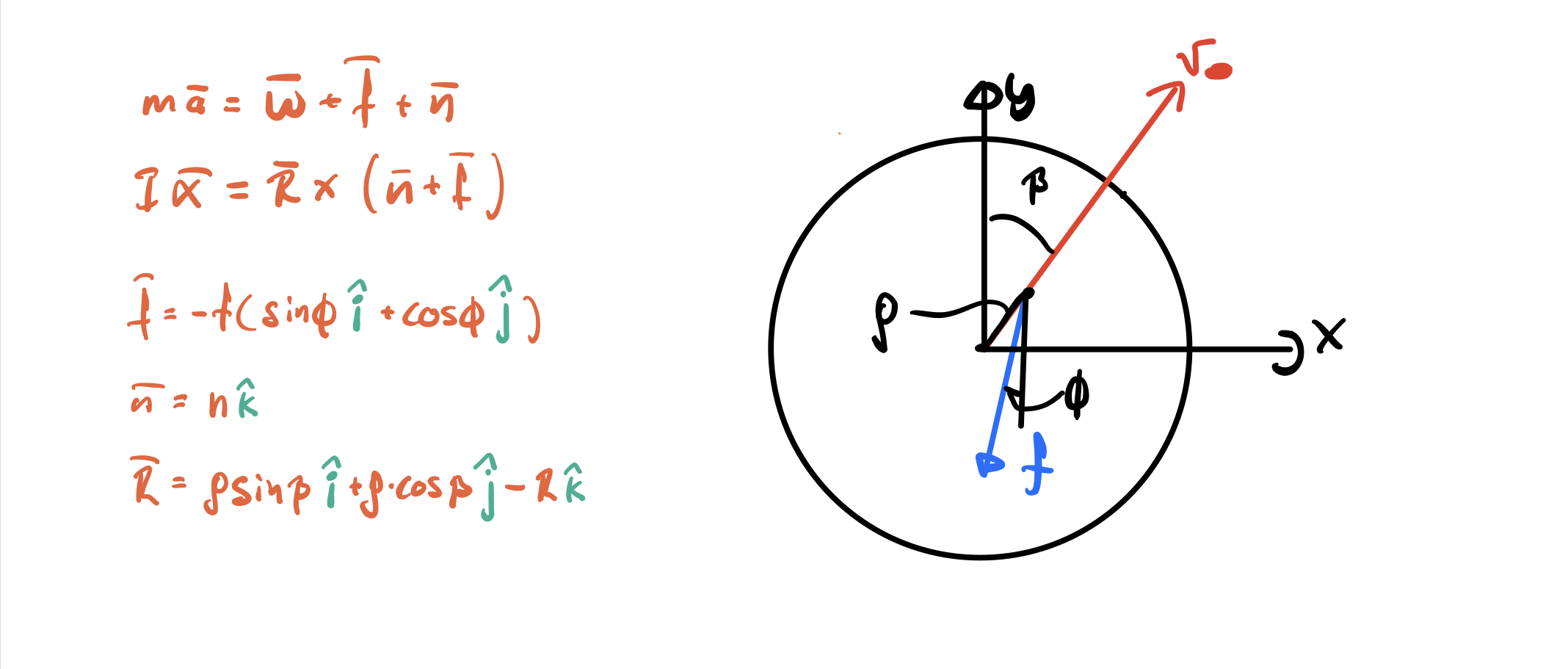
So far so good, or is it really? The term "w" in the above equations has not been mentioned. In this case the "w" is the forces of gravity acting on the golf ball. This term does take some extra effort to get right but have not fear. As mentioned just previously, the z-axis is normal to the surface of the green. This can be seen in the picture below.
The quest is now to express the force from gravity in the coordinate system with the z-axis acting as normal to the putting surface. To do this, the idea of coordinate transformation can be used, where in this case, no rotation around the z-axis is done. This results in the following rotational matrix and will give the "w" term according to:
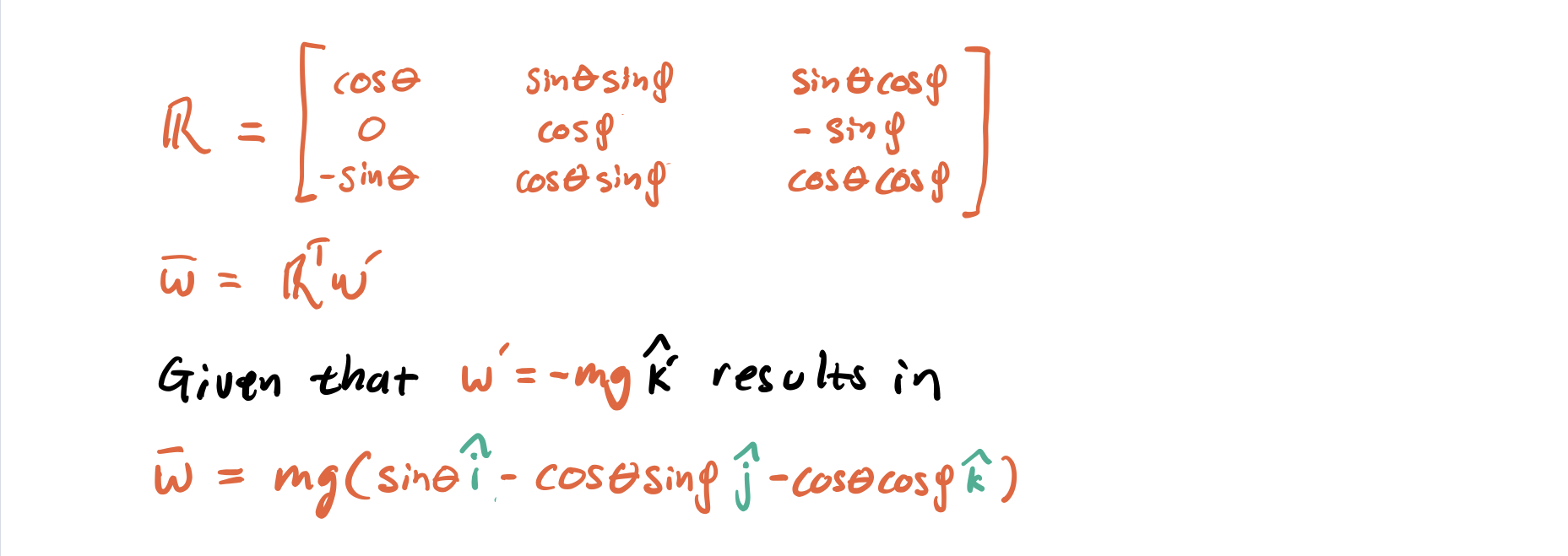
All right! Now all the equations needed to solve the problem has been established. But to be on the safe side, the above information can be summarised in the following set of equations:
Now it is time to do some grinding with the aim to extract expressions for the accelerations in x- and y-direction. After grinding this through, some rather simple expressions for the accelerations appear. They can be seen below.
Alright! So far, there has not been that much "computation" going on. But have no fear,
Python will come to the rescue. Since the accelerations has been established, standard ODE tools can be used
to solve the system. Let’s start by constructing a function that for a given input
(such as position and velocity but also the slope of the green and so on) delivers the accelerations.
Here, a trick of variable substitution is used to be able to solve second order differential equation using standard ODE tools.
"Putting" it all together in Python
Creating a Python function that do this is not too difficult. Below you see the code.
What now is left is to solve this system. This can be done by the code below. In this example, a golfer is trying to make a put on a green that slopes sideways by four degrees. Needed input parameters are taken from this article.
To test out the code, let’s try to create one of those cool plots that can be seen on the Golf Channel. Imagine trying to hole out a 4 meter putt with the same slope as mentioned above. One option could be to just give the ball enough speed to reach the hole. Another option could be to give it enough speed to travel approximately one meter past the hole. Given the two scenarios, a "corridor" can be plotted. This can be seen in the animation below.
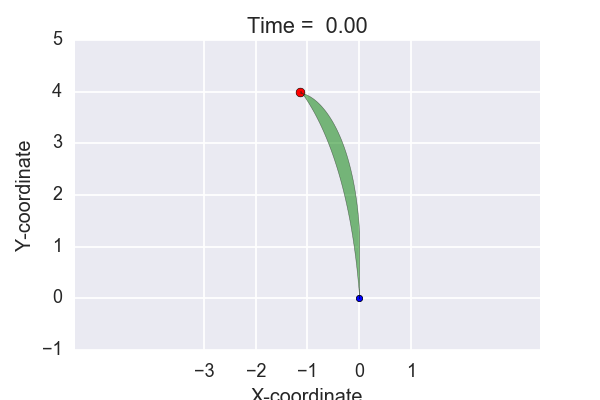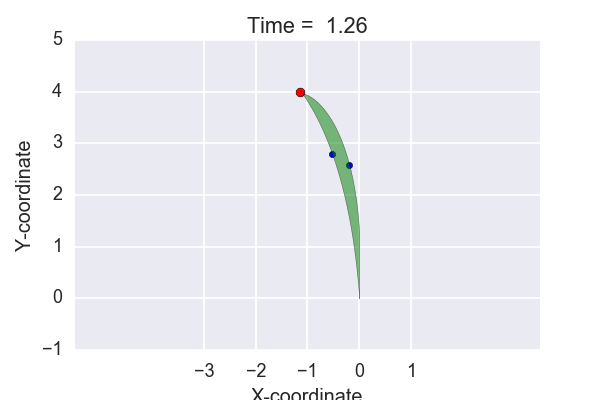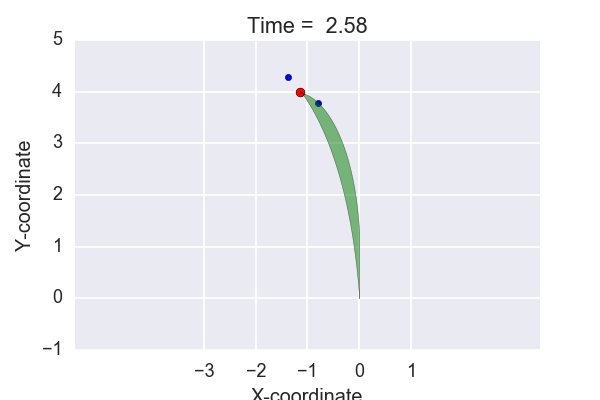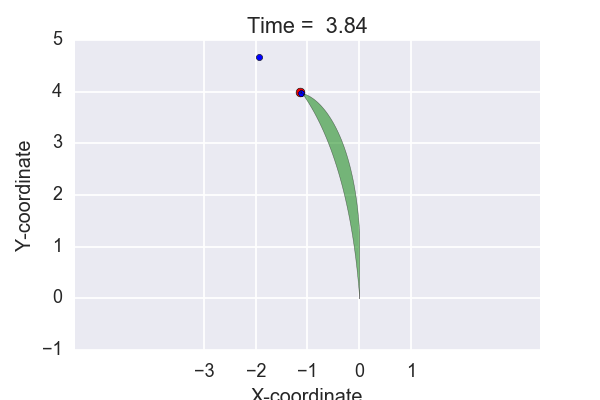
Time to conclude
This has been a post with rather much "non computational" content, but this was needed to find what equations to solve. There will be a second part of "Putting your putting skills to the test", with more "computational" focus, stay tuned.
That’s it! Hope you enjoyed the post and as always, contact us if you have some questions or comments.