Hi all, time for a new blog post! In this post we are going to look at a SAT question from 1982 that every student got wrong!!! I know, sound very unlikely. It was formulated like this:
In the figure above, the radius of circle A is 1/3 the radius of circle B. Starting for the position shown in the figure, circle A rolls around circle B. At the end of how many revolutions of circle A will the center of the circle first reach its starting point?
And the answers to choose from was:
- 3/2
- 3
- 6
- 9/2
- 9
Okay sounds kind of tricky but not impossible... For sure, the time is limited during this kind of tests so you could probably only spend a minute or so to solve it, but come on, at least someone should have guessed the correct answer.
So perhaps we should start with the reason why everyone got this question wrong, the correct answer is not among the alternatives A to E above...
Let's spend some more time on this question in order to arrive at the correct answer. To do so we start by looking at a simpler problem and see what we can learn.
Time to Simplify (but not too much...)
Let's start by "cutting" the large circle open and turn it into a flat line like in the picture below.
Just to make things as easy as possible we have assumed that the radius of the larger circle (circle B in the problem description) is \(r_L = 3 \) and the radius of the smaller circle is \(r_S = 1 \). The length of the flat line is equal to the circumference of the large circle i.e \( O_L = 2r_L\pi = 6\pi \) and the three different color segments all have a lenght that is equal to the circumference of the small circle i.e. \(O_S=2r_S\pi = 2\pi \). Moreover, we have added four "spokes" to the small circle to simplify the tracking of how many revolutions it has made.
Now let's start "transporting" the small circle along this line. The first thing we are going to do is just to slide the small circle along the line meaning that the same point on the small circle will be in contact with the line for the entire time

That seems ok, since it is always the same point on the circle that is in contact with the line the circle will not make any rotation.
So, now we continue with the situation where the circle will roll along the line. The funny thing when an object is rolling along a surface is that the speed of the point that is in contact with the line (in this case) is zero. We can use this in order to establish a relationship between how for the circle has traveled and how much it has rotated. To do so let's draw a small picture like the one below.
Here the \(s\) and \(v\) reprecents the distance the center has traveled and the speed of the center. Moreover, the \(\alpha\) and \(\dot{\alpha}\) is the angle and angular velocity, respectively. Now, since the speed of the contact point between the circle and the line (marked by an orange dot) is zero the following relation must hold.
\[ v + \dot{\alpha} \cdot r_S = 0 \Rightarrow v = - \dot{\alpha} \cdot r_S \]
Then we just integrate this thing in time we will get the relation between the distance the small circle have traveled and how much it has rotated i.e.
\[ s = -\alpha \cdot r_S \]
Nice! not that complicated if we apply this it would look something like this

Interesting! Perhaps not that surprising that the small circle have made 3 revolutions when it reaches the end of the line. This represents the ratio between the length of the line, \( 6\pi \) and the circumference of the small circle, \(2\pi\)
So, if we cut the lage circle open, flatten it to a straight line and roll the small circle along this distance the small circle will make 3 revolutions. I guess that this is why one of the possible answers to this question was 3 (alternative B in the original question above). However, this is not the correct answer to the original question where the large circle is a circle and not a flat line as we have studied here.
Let's get back to the original question and see what we can learn.
You Spin Me Round (Like a Record)
To start with, let's make a similar plot as the one we did above but for the case where the large circle is, in fact, a circle. It would look something like this
Just as above we have added the four spokes to the small circle and colored three different sections of the large circkle where each circle segment has the samle length as the circumfrence as the small circle.
Now, just as above let's start by sliding the small circle around the larger circle i.e. the same point of the small circle is in contact with the larger circle for the entire time. It would look like this:
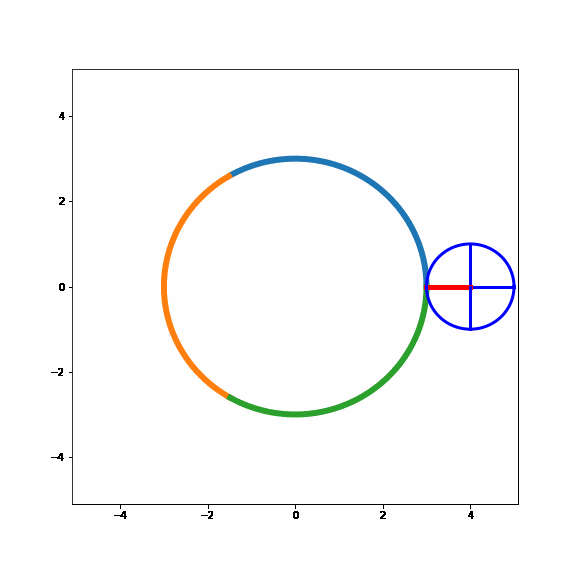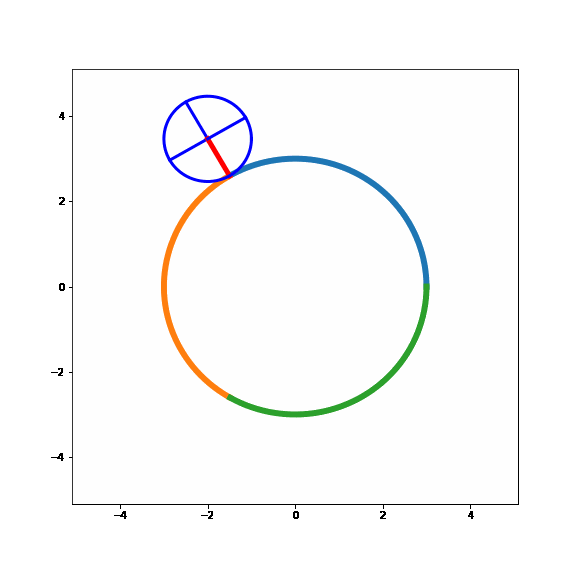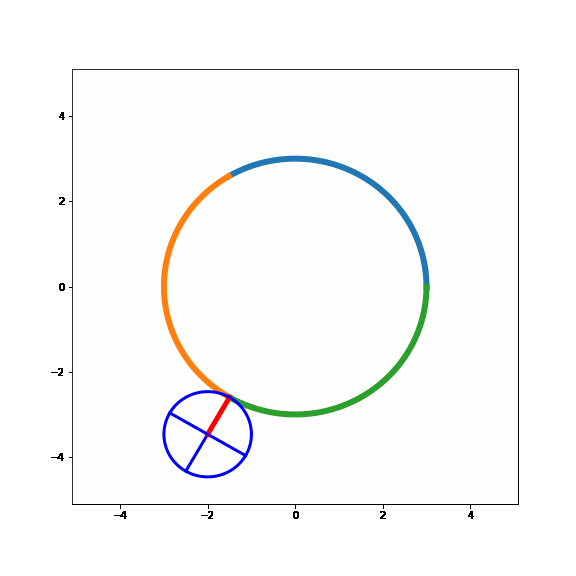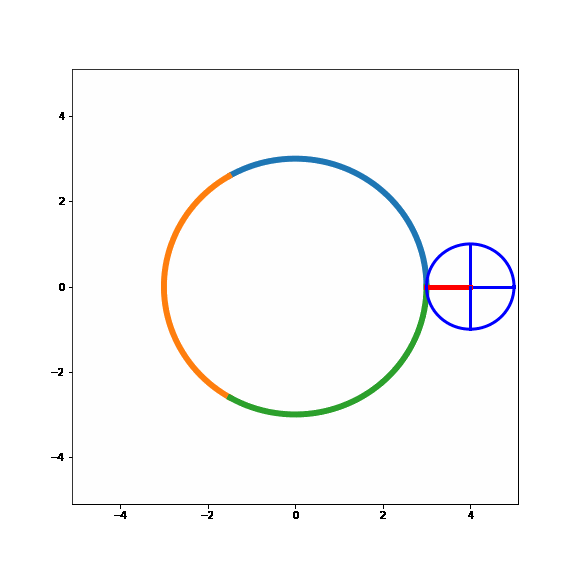
Ok, this looks a bit different than the simplified example above with the straight line... Even though we have slipped the small circle around the large circle, the small circle has made one complete revolution.
Now, we can start to see what the correct answer to the original question might be but let's just continue to "simulate" the situation where we roll the small circle around the large one.
Just as discussed above, the speed of the contact point between the small and the large circle is zero i.e. no slippage. Let's use this fact and draw a small picture and try to find out some relationships
Similar as above we integrate this in time and insert the values of \(r_L\) and \(r_S\) we get this relationship
\[ \alpha_S = 4 \cdot \alpha_L \]Super, after some simplifications the relation between \(\alpha_L\) and \(\alpha_S\) is quite simple. Let's see what this would look like.
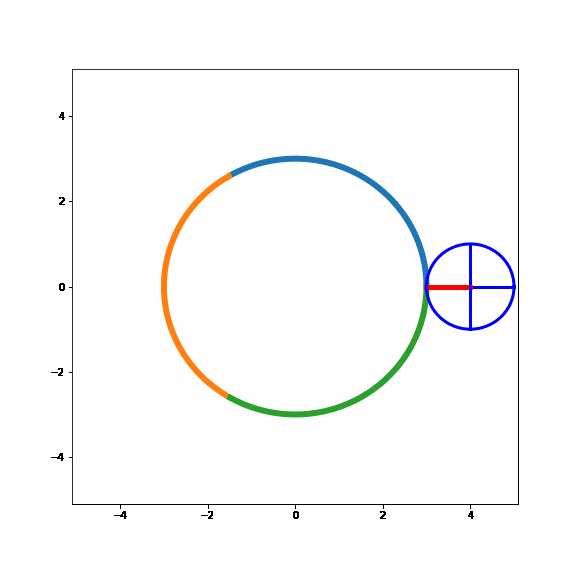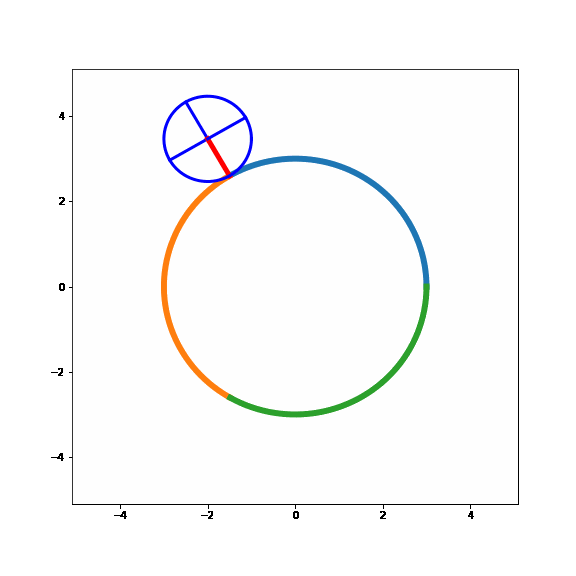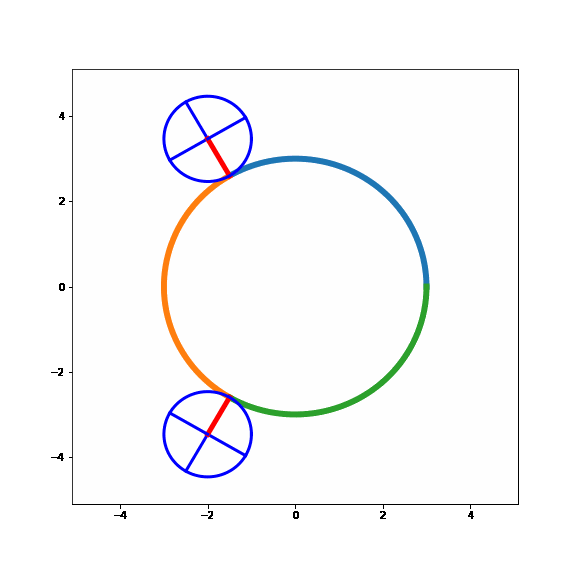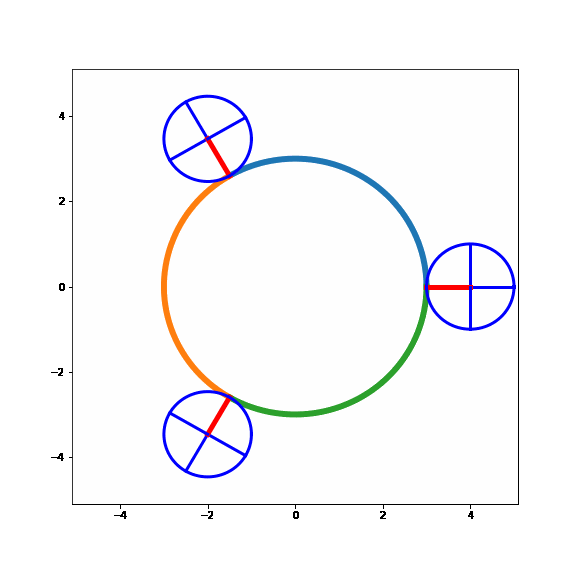
Nice!! It seems like the model behaves as expected. A specific point on the small circle will face the large circle three times during its path around the large circle, just like the example above where the small circle rolled along a straight line.
Now, the only thing left to do is to count how many revolutions the small circle makes on its path around the large one, should be quite easy.
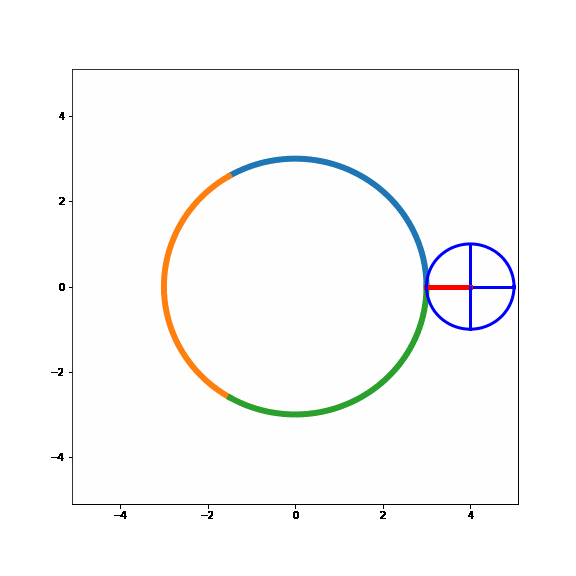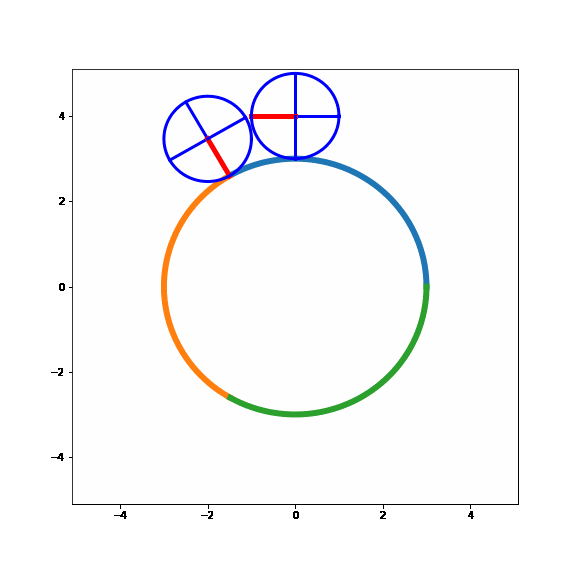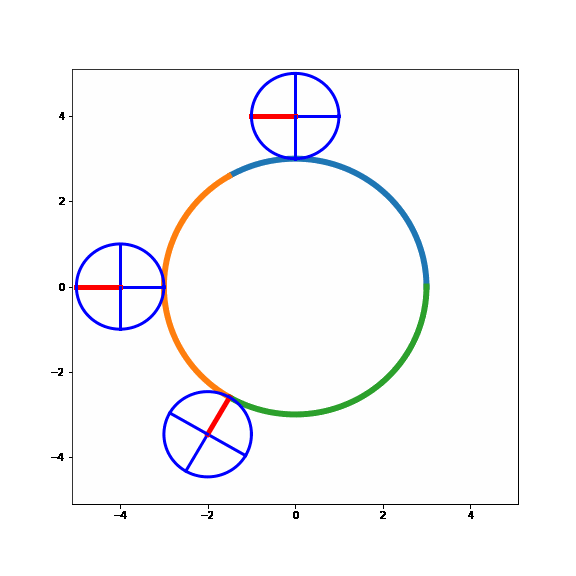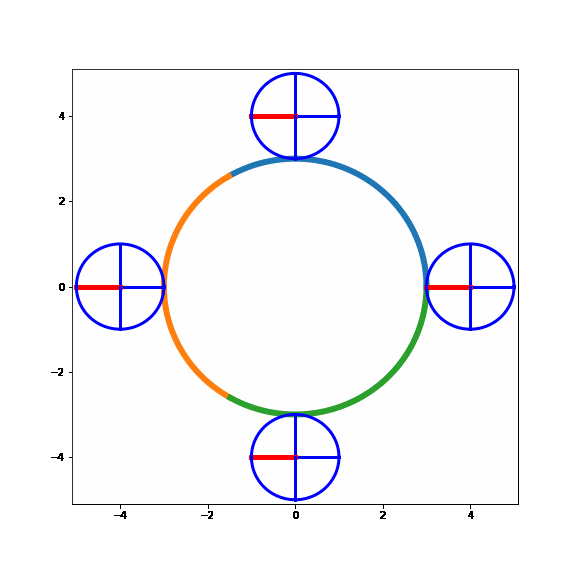
So the correct answer to the SAT question is 4 complete revolutions!
Time to Conclude
For sure this took much longer time than the time that was available during the actual test but at least we got the correct answer. I think that doing the example where the smaller circle is just sliding along the large circle is quite usefull to see that there is an "additional" revolusion added to the number of revolution calculated using just the ratios between the circumferences of the two circles.
Back in 1982 when the test was conducted there were a few students who noticed the mistake so the question was not included in the students total SAT score
Well I guess that was all for this time and, as always, feel free to contact us at info@gemello.se